Methodik: Mathe und mehr Mathe

Das Framework PRISMS stellt einen neuartigen, mathematisch fundierten Ansatz zur robusten multimodalen Segmentierung dar – mit besonderem Fokus auf die Herausforderungen der Gehirntumorsegmentierung. Für jede der verwendeten Modalitäten (Flair, T1ce, T1, T2) werden eigenständige 3D-Encoder eingesetzt, die charakteristische Feature-Tensoren

\[ F_m \in \mathbb{R}^{c \times h \times w \times d} \]

extrahieren. Ein gemeinsamer Decoder \(D_{\text{reg}}\) projiziert diese modalitätsspezifischen Features in einen gemeinsamen latenten Raum, was hilft, einen dominanzbasierten Bias zu vermeiden.

Im Kern ermöglicht der Adaptive Fusion Transformer (AFT) die integrative Fusion der modalitätsspezifischen Informationen, selbst wenn einzelne Modalitäten fehlen. Durch den Einsatz lernbarer Fusionstokens und einer speziell entwickelten modality-masked attention werden die Eingabefeatures, ergänzt durch Positionsembeddings, in einen gemeinsamen Token-Set \(Z_0\) überführt und über mehrschichtige Self-Attention-Mechanismen angereichert.

Ergänzend dazu wird mithilfe der Spatial Relevance Attention sichergestellt, dass die relevanten räumlichen Informationen gezielt hervorgehoben werden – indem aus den Attention-Matrizen gewichtete, räumliche Wichtigkeitskarten generiert werden. Der Kanalbezogene Fusionstransformer (KFT) ergänzt diesen Prozess, indem er kanalbezogene Redundanzen minimiert und mithilfe konvolutionaler Projektionen lokale Zusammenhänge beibehält.

Schließlich wird ein fünfstufiger Decoder \(D_{\text{fusion}}\) eingesetzt, der mit Hilfe von optimierten Skip-Connections – bei denen die Features vor der Fusion durch SRA und KFT verfeinert werden – und Deep Supervision zu hochpräzisen Segmentierungsergebnissen führt.

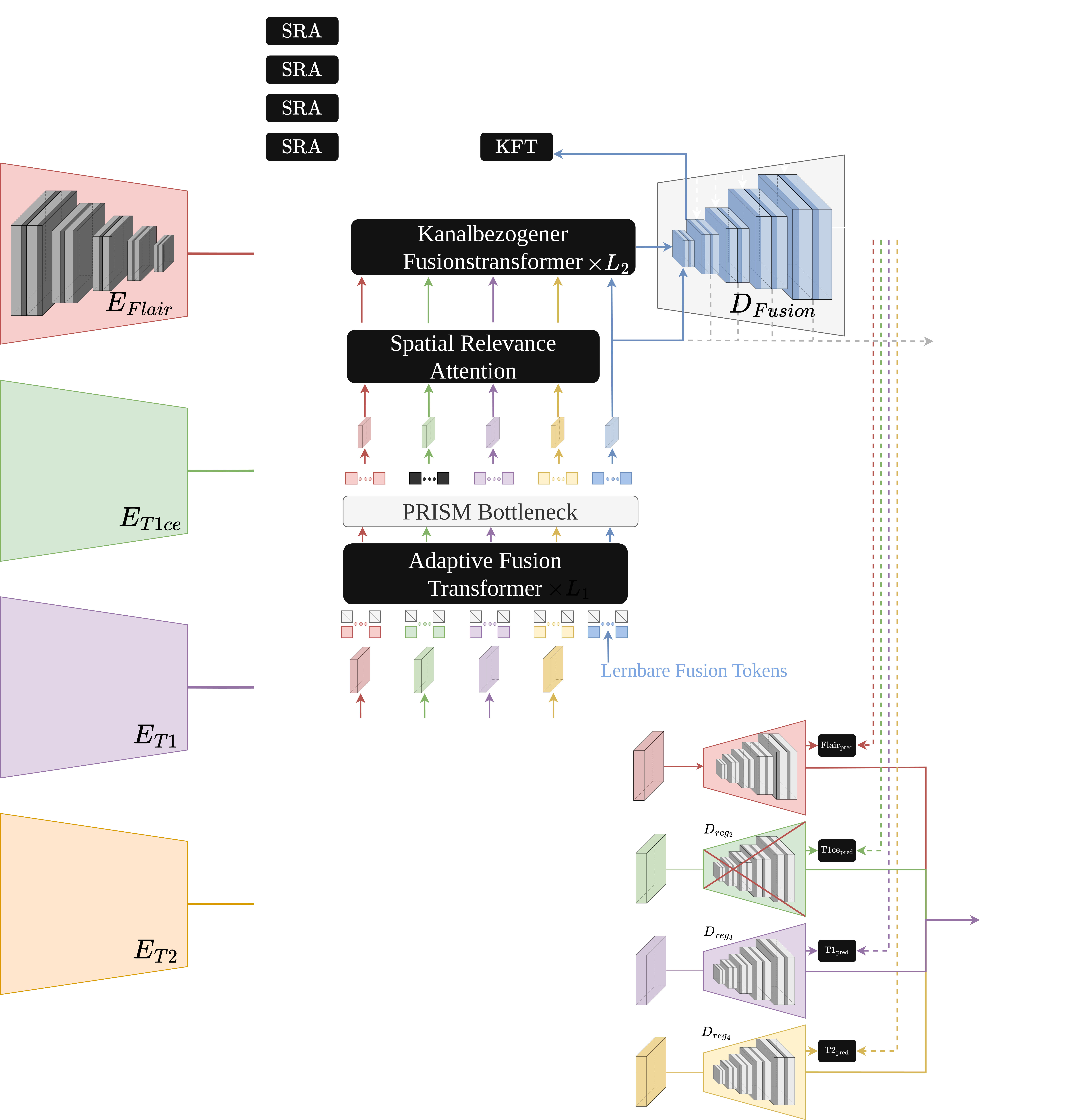
Überblick PRISMS

Modalitätsspezifische Feature Extraction

Gegeben sei die Menge der verwendeten Modalitäten

\[ M = \{\text{Flair}, \text{T1ce}, \text{T1}, \text{T2}\}, \]

wobei für jede Modalität \(m \in M\) ein 3D-Eingabepfad \(x_m\) vorliegt, der durch eine zugehörige Ground-Truth-Annotation \(y\) ergänzt wird. Zur Extraktion von modalitätsspezifischen Eigenschaften wird für jede Modalität ein eigenständiger Encoder \(E_m\) eingesetzt – strukturell angelehnt an die Architektur des 3D-UNet. Dieser Encoder wandelt den Eingabepfad \(x_m\) in einen Feature-Tensor um:

\[ F_m \in \mathbb{R}^{c \times h \times w \times d}. \]

Üblich ist in multimodalen Ansätzen die direkte Fusion der verschiedenen \(F_m\) gefolgt von einem Decoder, der auf Basis der kombinierten Information arbeitet. Allerdings hat sich gezeigt, dass ein solcher Ansatz dazu tendiert, vor allem die Modalität zu priorisieren, die die stärksten Merkmale liefert. Dies führt im Fall eines Ausfalls oder einer Qualitätsminderung genau dieser Modalität zu einer erheblichen Verschlechterung der Segmentierungsleistung.

Um diesem Modalitätsbias entgegenzuwirken, wird ein geteiltes Decoder-Modul \(D_{\text{reg}}\) eingeführt. Dabei werden alle modalitätsspezifischen Features in einen gemeinsamen latenten Raum projiziert, und jede Modalität wird anschließend separat für die Segmentierungsaufgabe optimiert. Das Trainingsziel dieser Architektur wird über den folgenden Verlust ausgedrückt:

\[ \mathcal{L}_{\text{reg}} = \sum_{m \in M} \Bigl( \mathcal{L}_{\text{Dice}}\bigl(D_{\text{reg}}(E_{m}(x_{m})), y\bigr) \;+\; \mathcal{L}_{\text{WCE}}\bigl(D_{\text{reg}}(E_{m}(x_{m})), y\bigr) \Bigr), \]

wobei \(\mathcal{L}_{\text{Dice}}\) den Dice-Verlust und \(\mathcal{L}_{\text{WCE}}\) den Weighted Cross Entropy Loss repräsentiert. <>

Adaptive Fusion Transformer

Transformer-Modelle haben sich als sehr effektiv erwiesen, wenn es um die Erfassung von Langzeitabhängigkeiten geht – ein entscheidender Vorteil im Rahmen der modalitätsübergreifenden Merkmalsextraktion. Dennoch ist die direkte Konkatenation und lineare Projektion der Features unterschiedlicher Modalitäten in Queries (Q), Keys (K) und Values (V) sehr anfällig, wenn Modalitäten fehlen.

Um diese Problematik zu adressieren, werden lernbare Fusionstokens eingeführt. Analog zu den Tokens aus dem Vision Transformer (ViT) [1], die als dynamische Embeddings für die Klassifikation dienen, ermöglichen diese Fusionstokens die Integration von Informationen aus allen verfügbaren Modalitäten. Der Adaptive Fusion Transformer (AFT) nutzt diese Tokens, um robust auch bei unvollständigen Eingaben eine effektive Featurefusion zu erzielen.

Zunächst werden die modalitätsspezifischen Features

\[ F_{\mathrm{m}} \in \mathbb{R}^{c \times h \times w \times d} \]

vom jeweiligen Encoder \(E_{\mathrm{m}}\) in eine 2D-Darstellung überführt:

\[ F_{\mathrm{m}} \in \mathbb{R}^{N \times c} \quad \text{mit} \quad N = h \times w \times d. \]

Zusätzlich wird ein Satz lernbarer Fusionstokens

\[ F_{\mathrm{fusion}} \in \mathbb{R}^{N \times c} \]

definiert. Durch Verkettung der Features aller Modalitäten und der Fusionstokens entsteht ein gemeinsamer Tensor

\[ F_{\mathrm{multi}} \in \mathbb{R}^{5N \times c}. \]

Unter Hinzunahme von lernbaren Positionsembeddings \(PE \in \mathbb{R}^{5N \times c}\) ergeben sich die finalen Feature-Embeddings, die als Input in den AFT eingespeist werden:

\[ Z_0 = F_{\mathrm{multi}} + PE. \]

Der AFT berechnet dann mithilfe einer speziell entwickelten modality-masked attention die Self-Attention. Dabei gilt:

Modalitätsspezifische Verfeinerung: Tokens, die zur gleichen vorhandenen Modalität gehören, interagieren ausschließlich miteinander.
Fusion über Modalitäten: Die Fusionstokens \(F_{\mathrm{fusion}}\) können über Self-Attention auf alle vorhandenen modalitätsspezifischen Tokens zugreifen, um eine globale Featurefusion zu ermöglichen.
Maskierung fehlender Modalitäten: Durch eine binäre Maske \(\mathcal{M} \in \{0,1\}^{5N \times 5N}\) werden alle Abhängigkeiten ausgeschlossen, bei denen ein Token aus einer fehlenden Modalität stammt.

Die modality-masked attention wird konkret folgendermaßen berechnet:

\[ \text{MA}(Q,K,i,j)= \frac{ \mathcal{M}_{i,j}\, \exp\Bigl(\frac{q_i\,k_j^T}{\sqrt{c/H}}\Bigr) }{ \displaystyle \sum_{\substaWT \[ \begin{aligned} Z'_0 &\leftarrow \text{MA}(Q,K)\cdot V, \\ Z_1 &\leftarrow \text{MHMA}(Z'_0) + Z_0, \\ Z_1 &\leftarrow \text{FFN}(\text{LN}(Z_1)) + Z_1. \end{aligned} \]

Nach \(L_1\) aufeinanderfolgenden AFT-Layern wird der Satz Fusionstokens aktualisiert und in die ursprüngliche 3D-Struktur zurückgeführt:

Die Fusionstokens werden zu \(\hat{F} \in \mathbb{R}^{c \times h \times w \times d}\) reshaped, sodass sie cross-modale Informationen enthalten.
Gleichzeitig werden die modalitätsspezifischen Feature-Tokens \(F_m \in \mathbb{R}^{N \times c}\) in \(\hat{F}_m \in \mathbb{R}^{c \times h \times w \times d}\) zurücküberführt, um mehr globalen Kontext innerhalb der jeweiligen Modalität abzubilden.

Hier ist eine erweiterte Version des Absatzes, die die Details zu den \(L\) Schichten sowie Verweise auf “Going Deeper” beibehält:

PRISMS im Detail

Spatial Relevance Attention

Während die modality-masked Attention sicherstellt, dass Tokens primär der eigenen, vorhandenen Modalität zugeordnet werden, erhalten alle Tokens zu Beginn dieselbe Gewichtung. In der Praxis trägt jedoch nicht jedes Token gleich stark zur Informationsfusion bei – besonders in tiefen Transformer-Architekturen, die aus \(L\) aufeinanderfolgenden Fusion-Layern bestehen. Wie in Going Deeper with Image Transformers [3] gezeigt wurde, tendieren Self-Attention-Matrizen in tieferen Schichten dazu, eine eher uniforme Gewichtsverteilung aufzuweisen. Deshalb wird bereits in der ersten Fusion-Schicht ein signifikanter Teil der relevanten Information extrahiert, der später in den weiteren \(L - 1\) Schichten stabilisiert wird.

Im ersten AFT-Layer wird daher die Attention-Matrix \(\text{MA}_1\) herangezogen, um die räumliche Relevanz der Tokens zu quantifizieren. Für jeden Token \(j\) wird dessen gewichtete Wichtigkeit durch Aufsummieren der Einträge aller Heads über die Zeilen, die den Fusionstokens zugeordnet sind (also \(i\) von \(4N+1\) bis \(5N\)), wie folgt berechnet:

\[ \text{Col}(j) = \sum_{H} \sum_{i=4N+1}^{5N} \text{MA}_1(i, j), \quad j \in [1, 4N], \]

wobei \(N = h \times w \times d\) die Anzahl der räumlichen Positionen angibt und die ersten \(4N\) Spalten die modalitätsspezifischen Tokens repräsentieren. Der resultierende Vektor \(\text{Col} \in \mathbb{R}^{1 \times 4N}\) wird anschließend für jede Modalität \(m \in M\) in Teilsegmente

\[ \text{Col}_m \in \mathbb{R}^{1 \times N} \]

aufgeteilt. Jedes dieser Segmente wird in eine räumliche Wichtigkeitskarte \(I_m \in \mathbb{R}^{1 \times h \times w \times d}\) reshaped. Diese Karte wird dann elementweise mit den modalitätsspezifischen Features \(\hat{F}_m\) verknüpft:

\[ \widetilde{F}_m = \hat{F}_m \odot I_m, \]

wobei \(\odot\) die elementweise Multiplikation kennzeichnet. Modalitäten, die nicht vorhanden sind, erhalten selbstverständlich eine Wichtigkeitskarte \(I_m = 0\), sodass sie keinerlei Einfluss auf die Fusion haben.

Darüber hinaus können diese räumlichen Gewichtskarten in den Skip-Connections integriert und an verschiedene Auflösungen angepasst werden, indem \(I_m\) mittels Upsampling transformiert wird. Durch diesen Mechanismus wird gewährleistet, dass schon in den ersten der \(L\) modality-masked Fusion-Layern die relevanten räumlichen Informationen extrahiert und an die nachfolgenden Schichten weitergegeben werden – ein entscheidender Faktor, um in tiefen Architekturen präzise Details zu erhalten.

Kanalbezogener Fusionstransformer

Obwohl die Spatial Relevance Attention effektiv räumliche Redundanzen zwischen den Tokens adressiert, können weiterhin redundante Informationen entlang der Kanäle in den Feature-Maps jedes Tokens auftreten. Um diese kanalbezogenen Überschneidungen zu minimieren und die relevanten Kanäle hervorzuheben, werden Kanalbezogene Fusionstransformer (KFT) zwischen den Fusionstokens und den modalitätsspezifischen Tokens eingefügt.

Konkret gilt Folgendes: Nach dem Adaptive Fusion Transformer (AFT) und der Spatial Relevance Attention erhält jede Modalität \( m \) verbesserte, modalitätsspezifische Features

\[ \widetilde{F}_m \in \mathbb{R}^{c \times h \times w \times d}. \]

Diese Features werden zunächst über die räumlichen Dimensionen reshaped, sodass

\[ \widetilde{Z}^m_0 \in \mathbb{R}^{c \times N} \quad \text{mit} \quad N = h \times w \times d \]

gewonnen wird. Für alle Modalitäten werden diese Reshapes anschließend entlang der Kanalachse konkateniert:

\[ \widetilde{Z}_0 = \mathrm{Konkat}\bigl(\widetilde{Z}^m_0 \,:\, m \in M\bigr) \in \mathbb{R}^{4c \times N}. \]

Parallel dazu werden die fusionierten Features aus dem AFT, \(\hat{F}_{\text{fusion}} \in \mathbb{R}^{c \times h \times w \times d}\), über die räumlichen Dimensionen in

\[ \hat{Z}_0 \in \mathbb{R}^{c \times N} \]

überführt. Diese Darstellung wird genutzt, um die Query-Repräsentationen \(Q\) zu berechnen, während \(\widetilde{Z}_0\) projiziert wird, um die Keys \(K\) und Values \(V\) zu generieren.

Da die Self-Attention hier kanalweise erfolgt und eine herkömmliche, vollverbundene (fully connected) Projektion über die räumlichen Dimensionen die ursprünglichen räumlichen Zusammenhänge verlieren würde, wird stattdessen ein lokal verbundenes, auf Convolution basierendes Projectionsschema verwendet. Dabei wird die Projektion gruppenspezifisch für jede Modalität entlang der Kanaldimensionen durchgeführt. Genauer wird der Projektionsprozess wie folgt formuliert:

\[ \begin{aligned} Q &= \Psi_q(\hat{Z}_0), \\ K &= \mathrm{Konkat}\bigl(\Psi_k^m(\widetilde{Z}^m_0) \,:\, m \in M\bigr), \\ V &= \mathrm{Konkat}\bigl(\Psi_v^m(\widetilde{Z}^m_0) \,:\, m \in M\bigr). \end{aligned} \]

Hierbei setzt sich jede Projektion \(\Psi_{\alpha}\) (für \(\alpha \in \{q, k, v\}\)) aus einer Folge von drei aufeinanderfolgenden Operationen zusammen:

\[ \Psi_{\alpha}(\cdot) = \phi_{\alpha}\bigl(\psi_{\alpha}\bigl(\varphi_{\alpha}(\cdot)\bigr)\bigr). \]

Dabei gilt:

\(\varphi_{\alpha}(\cdot)\) ist eine point-wise Convolution (Kernelgröße 1), die jeden Token einzeln abbildet und erste Feature-Präsentationen erzeugt.
\(\psi_{\alpha}(\cdot)\) fungiert als depth-wise Convolution mit einem Kernel der Größe 3, um lokale, kanalbezogene Zusammenhänge zu erfassen und den räumlichen Kontext der Tokens zu berücksichtigen.
\(\phi_{\alpha}(\cdot)\) übernimmt abschließend eine weitere point-wise Convolution (Kernelgröße 1), um die finalen Projektionseffekte zu erzielen.

Durch diesen zweistufigen Convolution-Ansatz bleiben die ursprünglichen räumlichen Informationen weitgehend erhalten, während gleichzeitig die kanalweise Relevanz dynamisch neu gewichtet wird. So kann der Kanalbezogene Fusionstransformer (KFT) effektiv redundante Informationen herausfiltern und zur globalen, konsistenten Merkmalsfusion über Modalitäten beitragen. Analog zur modality-masked attention wird hier eine binäre Maske über die Kanaldimensionen eingeführt, um kanalbezogene Redundanzen zu adressieren. Konkret definieren wir eine Maskenmatrix

\[ \mathcal{G} \in \{0,1\}^{c \times 4c}, \]

wobei jedes Element \(\mathcal{G}_{i,j}\) die Beziehung zwischen dem \(i\)-ten Element in der Query-Matrix \(Q\) und dem \(j\)-ten Element in der Key-Matrix \(K\) repräsentiert. Wird \(k_j\) einer fehlenden Modalität zugeordnet, so wird \(\mathcal{G}_{i,j} = 0\); andernfalls gilt \(\mathcal{G}_{i,j} = 1\).

Auf Grundlage dieser Maske definieren wir die kanalbezogene masked attention (KMA) wie folgt:

\[ \text{KMA}(Q,K,i,j)= \frac{ \mathcal{G}_{i,j}\, \exp\!\Bigl(\frac{q_i\,k_j^T}{\sqrt{N}}\Bigr) }{ \displaystyle \sum_{\substack{j' \\ \mathcal{G}_{i,j'}=1}} \exp\!\Bigl(\frac{q_i\,k_{j'}^T}{\sqrt{N}}\Bigr) }, \]

wobei \(N = h \times w \times d\) die Gesamtzahl der räumlichen Positionen darstellt.

Anschließend wird das Ergebnis der KMA mit einer Projektion \(\Psi_0\) weiterverarbeitet – analog zu den Projektionen \(\Psi_{\alpha}\) für \(\alpha \in \{q,k,v\}\) – und mit den ursprünglichen Fusion-Features \(\hat{Z}_0\) summiert:

\[ \widetilde{Z}_0 \leftarrow \Psi_0\Bigl(\text{KMA}(Q,K) \cdot V\Bigr) + \hat{Z}_0. \]

Im nächsten Schritt, im Feed-Forward-Block, wird ein convolutionaler Kernel mit einer Kernelgröße von 3 zwischen zwei vollständig verbundenen Schichten entlang der Kanaldimensionen integriert. Dieser Ansatz erfasst reichhaltige lokale (kanalbezogene) Informationen und aktualisiert gleichzeitig die ursprünglichen Fusion-Features \(\hat{Z}_0\). Das resultierende KFT-Layer wird dann wie folgt formuliert:

\[ \widetilde{Z}_1 \leftarrow \widetilde{\text{FFN}}(\hat{Z}_0) + \hat{Z}_0, \]

wobei \(\widetilde{\text{FFN}}\) das speziell entwickelte Feed-Forward-Netzwerk repräsentiert. Nach \(L_2\) KFT-Layern werden die Fusion-Features \(\hat{F}_{\text{fusion}} \in \mathbb{R}^{c \times h \times w \times d}\) weiter verfeinert und in \(\widetilde{F}_{\text{fusion}} \in \mathbb{R}^{c \times h \times w \times d}\) überführt. Diese Enhancement-Stufe basiert auf der simultanen räumlichen und kanalbezogenen Neugewichtung der modalitätsspezifischen Features, wodurch die cross-modale Informationsintegration weiter optimiert wird.

Decodierung mit Deep-Supervision

Zur Decodierung und Segmentierung wird ein fünfstufiger Decoder \(D_{\text{fusion}}\) eingesetzt, der strukturell dem gemeinsamen Regler-Decoder \(D_{\text{reg}}\) ähnelt, jedoch aus einer Folge von übereinandergestapelten konvolutionellen Blöcken besteht. Der wesentliche Unterschied liegt in den Skip-Connections: Hier fließen die Features aus den Encodern zunächst durch zusätzliche Gewichtungsschritte mittels Spatial Relevance Attention und kanalbezogener masked attention, bevor sie in \(D_{\text{fusion}}\) zusammengeführt werden.

Konkret werden die modalitätsspezifischen Features aus den Encodern – ergänzt durch die Verarbeitungsschritte des Adaptive Fusion Transformer (AFT), der Spatial Relevance Attention (SRA) und des Kanalbezogenen Fusionstransformers (KFT) – sequentiell verarbeitet, um hochqualitative Fusion-Features \(\hat{F}_{\text{fusion}}\) und \(\widetilde{F}_{\text{fusion}}\) zu erzeugen. Diese fusionierten Features werden anschließend konkateniert, upsampled und in den kanalbezogenen Fusion Transformer eingespeist, um mit den neu gewichteten Skip-Connection-Features, die ebenfalls über SRA generiert wurden, zu interagieren. Beginnend in den unteren beiden Ebenen des Decoders werden die fusionierten Features schrittweise hochskaliert und mit den entsprechenden Skip-Connection-Features progressiv zusammengeführt, bis der finale Output-Layer erreicht ist.

Der Decoder \(D_{\text{fusion}}\) wird mithilfe eines Segmentierungsloss trainiert, der wie folgt definiert ist:

\[ \mathcal{L}_{\text{seg}} = \mathcal{L}_{\text{Dice}}(D_{\text{fusion}}(\text{Konkat}(E_m(x_m))), y) + \mathcal{L}_{\text{WCE}}(D_{\text{fusion}}(\text{Konkat}(E_m(x_m))), y). \]

Um den Trainingsprozess zusätzlich zu stabilisieren und die Fusion-Features zu regulieren, wird Deep Supervision eingesetzt. Dabei werden die Fusion-Features aus jeder Stufe des Decoders – bezeichnet als \(\hat{F}^l_{\text{fusion}}\) für die \(l\)-te Stage – über ein Upsampling \( \text{Up}_{2^{l-1}} \) auf die originale räumliche Auflösung gebracht und anschließend mit entsprechenden Verlustfunktionen (Dice- und Weighted Cross Entropy Loss) beaufsichtigt:

\[ \mathcal{L}_{\text{ds}} = \sum_{l=1}^{5} \left[ \mathcal{L}_{\text{Dice}}(\text{Up}_{2^{l-1}}(\hat{F}^l_{\text{fusion}}), y) + \mathcal{L}_{\text{WCE}}(\text{Up}_{2^{l-1}}(\hat{F}^l_{\text{fusion}}), y) \right], \]

wobei \(\text{Up}_{2^{l-1}}\) ein Upsampling um den Faktor \(2^{l-1}\) darstellt. Dieser Ansatz der Deep Supervision sorgt für eine kontinuierliche Rückkopplung aus verschiedenen Auflösungsebenen, was zu einer stabileren Konvergenz und verbesserten Fusion der Features führt.

[1] Dosovitskiy, A., Beyer, L., Kolesnikov, A., Weissenborn, D., Zhai, X., Unterthiner, T., Dehghani, M., Minderer, M., Heigold, G., Gelly, S., Uszkoreit, J., & Houlsby, N. (2020). An Image is Worth 16×16 Words: Transformers for Image Recognition at Scale. arXiv preprint arXiv:2010.11929. doi:10.48550/arXiv.2010.11929

[2] Chen, J., Lu, Y., Yu, Q., Luo, X., Adeli, E., Wang, Y., Lu, L., Yuille, A. L., & Zhou, Y. (2021). TransUNet: Transformers Make Strong Encoders for Medical Image Segmentation. arXiv preprint arXiv:2102.04306. doi:10.48550/arXiv.2102.04306 (Hinweis: In PRISMS wird dieser Ansatz weiterentwickelt, um fehlende Modalitäten noch robuster zu kompensieren.)

[3] Touvron, H., Cord, M., Sablayrolles, A., Synnaeve, G., & Jégou, H. (2021). Going Deeper with Image Transformers. arXiv preprint arXiv:2103.17239. doi:10.48550/arXiv.2103.17239